In the past we received a reviewer’s comments using the two challenges to the “dark flow” measurement below. Although these challenges have already been addressed in detail in our peer-reviewed publications, we thus have prepared this webpage to provide rigorous scientific and technical rebuttals of these claims. We show below that our results are not affected by these claims.
The data to verify our measurements were posted at http://www.kashlinsky.info/bulkflows/data_public and numerous colleagues have written to us that they confirm the results displayed in the above URL exactly to all decimal places. The readers are urged to inspect the posted data and verify for themselves.
The two challenges that appeared in refereed literature as of 10/2011 are: 1) Keisler (2009, ApJ, 707, L42) has claimed that the dark flow induced CMB dipole is not statistically significant when reproducing our analysis with his own assembled cluster catalog, whereas 2) Osborne et al (2011, ApJ, 737, 98, hereafter OMCP) have introduced different filtering schemes, performed a substantially different type of analysis (see below) and claim not to detect the dark flow dipole. (Note that filtering is not a unitary operation, so the signal’s S/N depends on the filter used).
Both of these papers have been addressed – in fact, refuted - in mathematical and numerical detail in our peer-reviewed publications: 1) Atrio-Barandela et al (2010, ApJ, 719, 77 – AKEKE, available here) showed the error committed in Keisler’s analysis (see p83 and Fig. 5 of AKEKE); the spurious step identified there was confirmed by Ryan Keisler in private correspondence. 2) regarding the second challenge by OMCP, Kashlinsky et al (2011, ApJ, 732, 1 – KAE, available here) have shown that the cluster sample employed by OMCP gives a statistically significant measurement of the ``dark flow” contrary to the OMCP claim; KAE further identify the culprits of the OMCP analysis in p. 3, right column. (Fig. 1 of KAE further points out the explicit errors committed in v1 of OMCP).
We now discuss these two analyses in detail:
1. Keisler (2009) analysis
Ryan Keisler has replicated the KABKE1,2 analysis using a cluster catalog from public data. He confirmed the central dipole values measured by KABKE2, but claimed larger errors. AKEKE (Sec. 4 and Fig. 5) have since shown that the latter are due to Keisler not having removed the monopole and dipole from the CMB maps outside the CMB mask; the AKEKE identification was confirmed by Ryan Keisler in private correspondence. The figure below is taken from AKEKE (Fig. 5) and illustrates the difference when the dipole and the monopole are/are-not subtracted outside the mask (red/blue histogram lines respectively). Note how Keisler’s claimed errors are reproduced if the monopole and dipole subtraction is not done. In the latter case the S/N would decrease substantially, whereas for the correct processing of the data one recovers the measurement with S/N~3 (AKEKE).
Figure 1-K caption: Fig. 5 from AKEKE showing the histograms of the dipole in CMB maps outside the cluster. Note the differences in between proper processing (red lines) and the (significantly wider) distribution when the monopole and dipole are not removed outside the CMB mask as happened in Keisler (2009).
2. Osborne et al (2011, OMCP)
Osborne et al (2011, ApJ, 737, 98, hereafter OMCP) replicated our work on bulk flows, following the KA-B approach proposed by us (2000, ApJ, 536, L37) but using different filtering. Thus:
■ - OMCP use filters designed to detect radio point sources rather than remove the primary CMB, the main contaminant in the KA-B method and yet claim them to be “more accurate than the KABKE filter” which removes the primary CMB (the largest contributor to the error in the KA-B) method.
■ - The cluster catalog used by OMCP was assembled from public sources and cluster properties have not been homogeneously derived. X-ray luminosities of those public catalogs differ from SCOUT quite significantly in all ranges of X-ray cluster luminosities. See Fig. 2 of KAE.
■ - The predicted TSZ using the OMCP catalog is off by 30-50% [See OMCP Table 1] compared with the prediction from our catalog that has an uncertainty less than 10%.
■ - Our clusters extend to a radius for which the TSZ signal vanishes. OMCP fix the aperture at 15arcmin, allowing the TSZ component to contaminate their measurement [In Tables 3 & 4, their monopole is comparable or larger than any dipole component].
While OMCP confirm our results (but claim a slightly lower significance – see below) when reproducing our pipeline, their pipeline differs from ours in very significant respects and results in inconsistencies discussed below.
On OMCP Filters
■ - When choosing a filter to apply the KA-B method to a data set as noisy as WMAP all-sky maps, one must be very careful to remove the primary CMB while leaving the KSZ dipole signal intact. The CMB temperature field is comprised of several components, one of which represents the KSZ cluster signal producing a dipole due to a bulk flow. If the adopted filters decrease the KSZ component on a par with the other components (or more), one would not be able to measure the former. This is illustrated in the figure below taken from OMCP (their Fig. 13).
■ - We reproduce below Fig. 13 from OMCP to demonstrate this: OMCP-adopted filters begin to recover the velocity for V>6,000 km/sec (plus signs) or V>15,000 km/sec (blue diamonds). At those velocities, the KSZ signal of every single cluster could have been measured in the original (unfiltered) maps. Indeed the mean optical depth of their cluster sample if <tau>=7∙10-3, so the mean cluster KSZ signal is about dT~1,000 ľK: this means that OMCP should have measured KSZ signal quite easily directly from their unfiltered (simulated) maps; yet it is not measurable in their filtered maps.
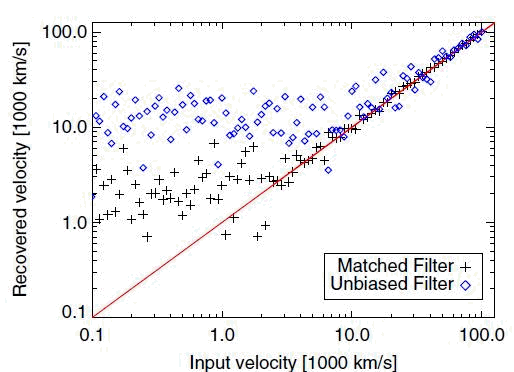Figure 1-OMCP caption: Fig. 13 from OMCP is reproduced here showing the recoverability (from simulations) of the input KSZ signal with their filters.
■ - OMCP filters reconstruct the KSZ signal from ℓ≥300, neglecting the 50-90 % of the signal present in the ℓ<300 range of multipoles and, at the same time, they boost the power at high ℓ's to account for the missing signal. While this procedure works on maps with only KSZ, it would render the method useless if the noise and residual CMB are added, since the latter two components, that dominate the error bar, are also boosted. As a result, their filters can measure a dipole when their sample of ~ 700 clusters is moving at almost relativistic speeds.
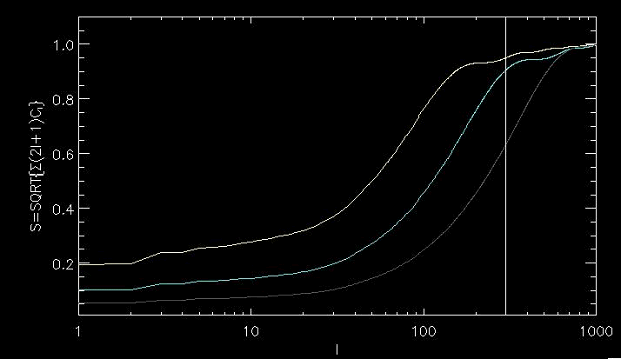Figure 2-OMCP caption: We measure a dipole at 600 clusters randomly distributed on the sky outside the CMB Kp0 mask. The contribution of each ℓ-multipole to the power of the dipole S in ℓ-space is S2(ℓ)=SUMi=2ℓ (2i+1)Ci. In the plot we see how the signal builds up. Green, yellow and grey lines correspond to clusters having 60, 30 and 15 arcmin radius. In all cases, more than 50% of the signal comes from multipoles ℓ<300. OMCP filters are lower pass filters, effectively removing power at ℓ<300, so OMCP are dismissing a large fraction (most, in fact) of the signal.
■ - Putting it differently, the OMCP filtering reduces the S/N of the KSZ signal. In our studies the result is recovered at S/N~4, which is highly statistically significant. But if filtering were to reduce the KSZ term by a mere factor of ~2 (see Figure 2-OMCP above), the S/N would drop below the statistically significant threshold. The figure demonstrates how critical it is to preserve the contributions from low ℓ’s in filtering (OMCP filters remove the contributions out to ℓ~300 – see their Fig. 3).
Inconsistencies in the OMCP error bars
■ - WMAP CMB mask removes more sky in the direction of the Galactic center and anticenter, so the errors in the X component of the dipole have to be larger than the Y or Z component (the latter will have the smallest error). This was proven analytically and confirmed numerically in AKEKE. However, the errors quoted by OMCP in their Tables 2-4 show the exact opposite and cannot be correct.
■ - OMCP never present their estimate of the errors based on eq. 1 of AKEKE. [We have asked for this simple computation, as it could have shed light on the inconsistencies we find in their tables, but OMCP have not provided the numbers.]
■ - OMCP compute their error bars using only 100 simulations, which leads to a 10% (at one standard deviation in their sigma’s) extra uncertainty in their error bars. In this respect, what they call a “2.9-sigma detection” with our filter (see below), is easily equivalent to ~(3-3.5)- sigma. (Our errors are based on 4,000 realizations in each simulation).
■ - OMCP never consider the fact that we are not measuring a dipole on a random direction, but in the direction of the CMB dipole, a very unlikely event (at the level of ~1%).
■ - When using our Wiener-type filter, OMCP recover our results [see their Tables 9 & 10] yet claim that their significance is, at most, ``at the 2.9-sigma confidence level". While clearly a "2.9-sigma" detected dipole constitutes a statistically significant result, other numbers point to more inconsistencies in their pipeline: e.g. as discussed above, in Table 9 & 10 the error on the X component is smaller than in the Y component, when WMAP masks remove more solid angle in the direction of the Galactic center and anticenter.
■ - OMCP compute the dipole at 15’ instead of at the zero monopole, thereby increasing the error bars and allowing the TSZ component to contaminate their measurement [see their Tables 3, 4].
■ - OMCP errors are computed from simulations instead of from the actual realization of the sky that, as was discussed in AKEKE, increases error bars by an extra 10-15%; the X-ray properties of their clusters were derived by combining different sources, increasing the uncertainty of their results [see for instance Fig 2 of KAE]. For comparison, their predicted TSZ monopole is 30 to 50% larger than the measured value [Table 1 of OMCP], compared with the prediction made from the SCOUT catalog that differ by less than 10% from the measurements. Then, their arguments about the optical depth of high luminous clusters [Appendix B.2] cannot be trusted.
October, 2011
 | | | | | delete
NO UNDOES!
deletes permanently |